How to calculate the weighted spherical average of multiple vectors

#vectors #manifolds #steering #vector-search #math #python

When working with neural networks, you sometimes want to combine multiple concept vectors using weighted averages. This can be useful for vector search, by combining multiple concepts into a single query vector (which is what most vector databases expect). Another application is for creating steering vectors to control the behavior of generative models.

One way to do this is to take the Euclidean mean and then unit-norm the result. For example if you have $v_{0} = [1, 0, 0]$ and $v_{1} = [0, 1, 0]$ (orthogonal vectors on the unit sphere), their average $(v_{0} + v_{1}) / | | v_{0} + v_{1} | |_{2} = [0.707, 0.707, 0]$ corresponds to the $45 °$ midpoint as expected.

This method works for a simple average of two vectors if they a small angular difference However, it breaks down when you have multiple vectors, larger angles, or want to do a weighted average.

For example, repeating the calculation using weights $[\frac{2}{3}, \frac{1}{3}]$ :

import numpy as np

def lerp(vectors, weights):
    """
    Linear interpolation between vectors plus a unit-norm.

    vectors: array of shape (n, d), unit length.
    weights: list or array length n, sums to 1.
    """
    # Calculate the euclidean weighted mean
    weighted_vecs = vectors.T @ weights
    # Project back onto the unit sphere
    avg_unit = weighted_vecs / np.linalg.norm(weighted_vecs)
    return avg_unit

vecs = np.array([[1, 0, 0], [0, 1, 0]])
weights = np.array([2/3, 1/3])
avg_unit = lerp(vecs, weights)

# Dot products give cosines of the angles b/w original vectors
# and the averaged vector
cosines = vecs @ avg_unit

# cos of angles -> radians -> degrees
angles_deg = np.degrees(np.arccos(cosines))

print(f"Lerp vector: {avg_unit}")
print(f"Lerp angles: {angles_deg}")

Lerp vector: [0.89442719 0.4472136 0. ]
Lerp angles: [26.56505118 63.43494882]

Uh oh. The vector is supposed to be $30 °$ and $60 °$ from the original vectors, but instead the angles are $26.5 °$ and $63.4 °$ .

The correct way to do this is using "slerp", which is a funny short-hand for "spherical linear interpolation". Slerp interpolates along the shortest act on a sphere, as opposed to "lerp" (linear interpolation) method we did previously. The formula for slerp is:

slerp (v_{0}, v_{1}, w_{0}, w_{1}) = \frac{\sin (w_{0} Ω)}{\sin Ω} v_{0} + \frac{\sin (w_{1} Ω)}{\sin Ω} v_{1}

Ω = \arccos (v_{0} \cdot v_{1})

or in Python:

def slerp(v0, v1, w0, w1):
    """Spherical linear interpolation between two vectors."""
    cos_theta = np.dot(v0, v1)
    # omega is the arc length or angle (in radians) between the two vectors
    omega = np.arccos(cos_theta)  # aka theta
    sin_omega = np.sin(omega)  # aka sin(theta)
    # Given the plane spanned by v0 and v1, if we want to rotate v0 towards v1 by a fraction w1
    # Dividing by sin(omega) normalizes the vector so that its length is 1.
    return (np.sin(w0 * omega) * v0 + np.sin(w1 * omega) * v1) / sin_omega

interp_vec = slerp(vecs[0], vecs[1], weights[0], weights[1])

# Verify the angle
cos = vecs[0] @ interp_vec
angle_deg = np.degrees(np.arccos(cos))

print(f"Slerp vector: {interp_vec}")
print(f"Slerp angle: {angle_deg:.1f}")

Slerp vector: [0.8660254 0.5 0. ]
Slerp angle: 30.0

This is 30 degrees as expected. Let's plot this to see (plotting code here):

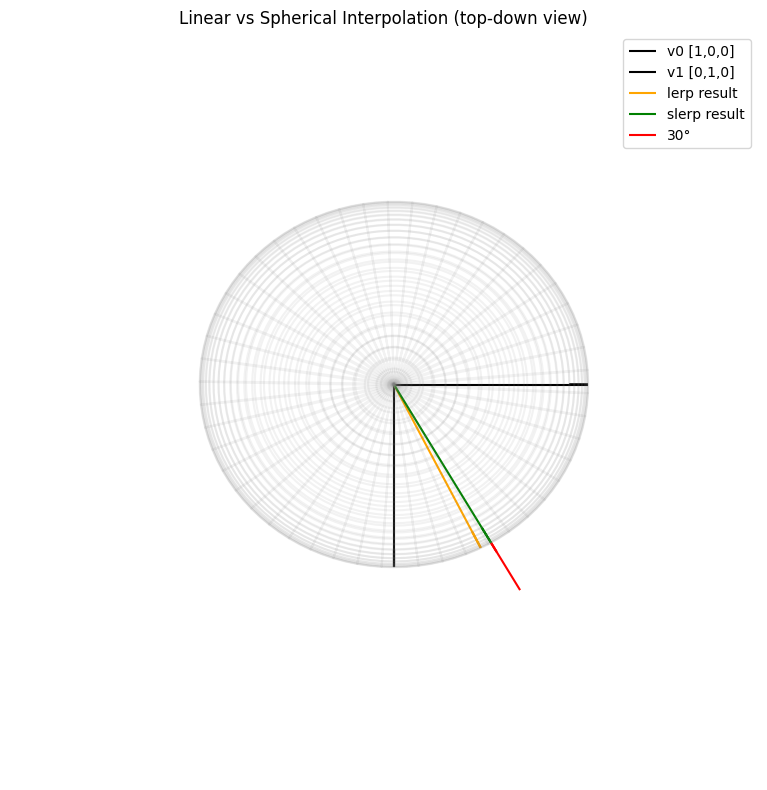
Great-- but how do we generalize slerp to many vectors? The goal is to find a vector $\vec{q}$ which minimizes the weighted sum of squared spherical distances between all the points on the d-sphere:

\vec{SphericalAvgVec} = \underset{q \in S^{d}}{argmin} \sum_{i} w_{i} θ (q, v_{i})^{2}

where $w_{i} \geq 0$ and $\sum_{i} w_{i} = 1$ .

Unfortunately, I couldn't find a closed-form solution to this problem, but this StackExchange post points to an iterative algorithm. The method is courtesty of "Spherical Averages and Applications to Spherical Splines and Interpolation" by Buss and Fillmoore (2001).

Here is algorithm A1 from the paper implemented in Python with the help of o3. I added a ton of explanation throughout because my trigonometry was embarassignly rusty:

def spherical_weighted_average(points, weights, tol=1e-12, max_iter=100):
    """
    Buss & Fillmore algorithm: weighted spherical mean with multiple vectors.

    Implementation of Algorithm A1. 

    points  : (n, d+1) unit vectors
    weights : (n,) non-negative
    tol     : stop when update < tol
    max_iter: safety cap
    Returns : (d+1,) unit vector – the weighted spherical mean
    """
    # Cast to float arrays
    pts = np.asarray(points, dtype=float)
    w   = np.asarray(weights, dtype=float)
    w  /= w.sum()                       # normalise weights

    # Initial guess using linear interpolation and unit-norm
    q = lerp(pts, w)

    for _ in range(max_iter):
        # dot product of each point with the current guess.
        # For unit vectors, this is the same as the cosine of the angle.
        # The clipping is for numeric safety.
        cos_theta = np.clip(pts @ q, -1.0, 1.0)
        theta = np.arccos(cos_theta)  # the angle between each point and the current guess
        sin_th = np.sin(theta)  # will appear in the denominator later

        # Log map step: v_i = (θ_i / sin θ_i) * (p_i - cos θ_i * q)
        # slide each point back to the tangent plane at q using the scale coefficient theta/sin_theta
        # set coef to 1 wherever denominator is close to zero to avoid division by zero
        coef = np.where(sin_th > 1e-12, theta / sin_th, 1.0)
        # multiplying q by the dot(p, q) gives the component of each point in the direction of the current guess
        # subtracting this from p gives the vector orthogonal to q in the tangent plane of the sphere at q
        # the magnitude of this vector is sin_theta, so dividing by sin_theta rescales the vector to unit length 
        # while still pointing towards p.
        # the true surface distance from q to p is theta. so multiplying the unit vector by theta stretches it 
        # to the same length as the arc length between q and p.
        v = coef[:, None] * (pts - cos_theta[:, None] * q)

        # Take the weighted average of the tangent vectors.
        # v is a tangent vector for each each input point.
        # this gives the steepest descent direction, reducing the total squared
        # spherical distance between the points and the current guess.
        # u lives in the q's tangent plane, i.e. q ⟂ u
        # it's magnitude is the distance to move along the sphere.
        u = (w[:, None] * v).sum(axis=0)

        # Done if the tangent step is tiny
        norm_u = np.linalg.norm(u)  # distance to move along the sphere
        if norm_u <= tol:
            break

        # exp map step: move the current guess q towards u by geodesic distance norm_u.
        # So, we have to rotate q in the plane spanned by q and u.
        # If we rotate q towards u by an angle, the resulting vector is:
        # q_new = cos(angle)*q + sin(angle) * u_normalized
        # Since the |u| is in radians, we can use this distance as the angle and plug it into:
        #     cos(|u|) q + sin(|u|) (u/|u|).
        q = np.cos(norm_u) * q + np.sin(norm_u) / norm_u * u
        q /= np.linalg.norm(q)  # should be unnecessary, but just in case

    return q

Now we can use slerp with more than two vectors:

vecs = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
weights = np.array([0.1, 0.3, 0.6])

spherical_mean_vec = spherical_weighted_average(vecs, weights)
print(f"Slerp vector: {spherical_mean_vec}")

# Verify the angles
angles_deg = np.degrees(np.arccos(vecs @ spherical_mean_vec))
print(f"Slerp angles: {angles_deg}")

lerp_vec = lerp(vecs, weights)
print(f"Lerp vector: {lerp_vec}")
angles_deg = np.degrees(np.arccos(vecs @ lerp_vec))
print(f"Lerp angles: {angles_deg}")

Slerp vector: [0.18928026 0.49047448 0.85065138]
Slerp angles: [79.08921607 60.62822759 31.71741214]
Lerp vector: [0.14744196 0.44232587 0.88465174]
Lerp angles: [81.52128685 63.74762488 27.79130564]

There's a small but significant difference :)

Copyright Ricardo Decal. richarddecal.com